Bisección
Bisección: dividir en dos partes igualesEl método de bisección busca un punto que este dentro del intervalo [a b], la busqueda de este punto se acerca sucesivamente a la solución. En este caso el punto nuevo calculado será el punto medio en [a b].
A continuación se presenta el pseudocódigo
Entradas
$f(x)$
$[a\ b]$
$N$
$e$
//------- Inicio
si $f(a)*f(b) == 0$ entonces
si $f(a) == 0$ entonces
$r \leftarrow a$
mensaje: "raiz encontrada"
sino
$r \leftarrow b$
mensaje: "raiz encontrada"
fin del si
sino
si $f(a)*f(b) > 0$ entonces
mensaje: "es probable que no halla raíz en el intervalo considerado"
sino
iterar $\leftarrow$ verdadero
$k \leftarrow 1$
mientras iterar
$r \leftarrow \frac{a+b}{2}$
si $f(a)*f(r) < 0$
$b \leftarrow r$
sino
$a \leftarrow r$
fin del si
$k \leftarrow k + 1$
si $k > 1$ entonces
si $|b-a| < e$
iterar $\leftarrow$ falso
mensaje: "raiz encontrada"
fin del si
si $k > N$ entonces
iterar $\leftarrow$ falso
mensaje: "raiz no encontrada"
fin del si
fin del mientras
fin del si
fin del si
Ejemplo 1
Entradas
$f(x) = x^2+2x-5$
$a = 0$
$b = 2$
$N = 30$
$e = 0.000001$
Secante
El método de la secante es similar al de bisección en el sentido de que se busca un punto que este dentro del intervalo [a b], la búsqueda de este punto se acerca sucesivamente a la solución. En este caso el punto nuevo calculado sera el que surge de la intersección de la recta que une a los puntos (a,f(a)) y (b,f(b)) y el eje horizontal "x".
primero calculamos la pendiente de la recta
m = (f(b) - f(a))/(b - a); luego construimos la ecuación punto pendiente
y - f(a) = m*(x - a); definimos y = 0; luego despejamos "x", y obtenemos
x = a - f(a)/m; finalmente sustituimos el valor de m.
x = a - f(a)*(b - a)/(f(b) - f(a)).
A continuación se presenta el algoritmo de secante en pseudocódigo
f(x)
[a b]
N
e
inicio
si f(a)*f(b) == 0
si f(a) == 0
r <- a
mensaje: "raíz encontrada"
sino
r <- b
mensaje: "raíz encontrada"
fin del si
sino
si f(a)*f(b) > 0
mensaje: "Es muy probable que no halla raíz en el intervalo considerado"
sino
iterar <- verdadero
k <- 1
mientras iterar
r <- a - f(a)*(b - a)/(f(b) - f(a))
si f(a)*f(r) < 0
b <- r
sino
a <- r
fin del si
k <- k + 1
si k > 1
si |r(k)-r(k-1)| < e
si |r(k)-r(k-1)| < e
iterar <- falso
mensaje: "raiz encontrada"
fin del si
fin del si
fin del si
si k > N
iterar <- falso
mensaje: "raiz no encontrada aun"
fin del si
fin del mientras
fin del si
fin del si
figura 3: método de la secante
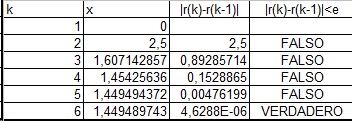
Ejemplo 2
Entradas:
f(x) = x^2+2*x-5; a = 0; b = 2; N = 20; e = 0.001
Tabla 2: búsqueda de la raíz de f(x) empleando el método de la secante
Salidas
Raíz encontrada
r = 1.4495
k = 5
Newton
El método Newton no considera un dominio [a b] dentro del cual se supone que existe una raíz de f(x). Este método inicia seleccionando un valor xo, el cual se asume como cercano a la raíz buscada. Luego se traza la recta tangente a f(x) en el punto (xo,f(xo)), y calculamos el punto x1, que resulta de intersectar la recta tangente hallada con el eje x.
primero calculamos la pendiente de la recta
m = f'(xo); luego construimos la ecuación punto pendiente
y - f(xo) = m*(x - xo); definimos y = 0; luego despejamos "x", y obtenemos
x = xo - f(xo)/m; finalmente sustituimos el valor de m.
x = xo - f(xo)/f'(xo).
Las entradas al algoritmo son:
f(x): funcion.
xo: punto inicial (aleatorio o arbitrario).
Nmax: numero máximo de iteraciones.
e: error
Salidas
r: raíz (de ser encontrada).
k: iteraciones alcanzadas.
e: error (al no alcanzar la raiz).
A continuación se presenta el algoritmo de Newton en pseudocódigo
f(x)
xo
Nmax
e
inicio
k = 1
si f(xo) == 0
mensaje: "raiz encontrada en xo"
sino
seguir = verdadero
mientras seguir
xk = xk-1 - f(xk-1)/f'(xk-1)
k = k + 1
si k > Nmax
seguir = falso
si e < |xk-1 - xk|
mensaje: "se supero Nmax, raíz no encontrada"
fin del si
fin del si
si e > |xk-1 - xk|
seguir = falso
si k < Nmax
mensaje: "raiz encontrada en xk"
fin del si
fin del si
fin del mientras
fin del si
figura 4: método de Newton
Ejemplo 3
Entradas:
f(x) = x^2+2*x-5; N = 20; e = 0.001
Salidas
Raíz encontrada
r = 1.4495
k = 6
Punto fijo
El método de punto fijo toma en cuenta que una función g(x) posee un punto fijo en p tal que g(p) = p, para hallar la raíz de una función f(x) = 0 esta se transforma obteniendo así una función g(x), por ejemplo, si sumamos x en ambos lados obtenemos x + f(x) = x, si x = p y x + f(x) = g(x), hemos obtenido entonces que g(p) = p, esto quiere decir que si la función g(x) tiene un punto fijo en p entonces f(x) = x - g(x), entonces f(p) = p-g(p).
el método del punto fijo comienza con la aproximación inicial xo, entonces x1 = g(xo), generalizando
x(k+1) = g(x(k))
Si g(x) es continua en [a b] para todo x en [a b] entonces es posible hallar un punto fijo p en [a b], si ademas g'(x) existe en ]a b[, es posible encontrar una constante c < 1, tal que: g'(x) <= c, para todo x en ]a b[, entonces el punto fijo de g en [a b] es único, también g'(x) es continua en [a b] y g'(x) <> 0, asi, para cualquier valor de xo en [a b] la secuencia x(k+1) = g(x(k)) converge a p y |x(k+1) - p| < c*|x(k) - p|
Considerando la función en estudio f(x) = x^2+2*x-5, en donde se desea obtener x tal que f(x) = 0, al despejar x podemos obtener dos funciones de la forma x = g(x), esto es:
1) x = (5-x^2)/2
2) x = (5-2*x)^0.5
Consideremos la secuencia de la función 1)
x1 = (5 -(xo)^2)/2
x2 = (5 -((5 -(xo)^2)/2)^2)/2
Observamos inmediatamente de que se trata de una secuencia creciente
Consideremos la secuencia de la función 2)
x1 = (5-2*xo)^0.5
x2 = (5-2*(5-2*xo)^0.5)^0.5
Observamos inmediatamente que se trata de una secuencia decreciente
Si igualamos f(x) = 0 y sumamos x en ambos lados..
x = x^2+3*x-5, observamos nuevamente una secuencia creciente.
Dejo al visitante la programación del método de punto fijo
