Cuando se tiene un conjunto de puntos que viene de un muestreo de datos, se construye una curva que se espera interprete el comportamiento de la tendencia de los datos muestreados. Se dice que este comportamiento es el modelo matemático del sistema fenomeno de donde se efectúan las mediciones.
Esta sección considerará únicamente datos en el plano cartesiano (x,y)
1.- Trazadores lineales
Sea un conjunto de puntos (x,y), esto es
$(x_0, y_0)$
$(x_1, y_1)$
$(x_2, y_2)$
:
:
:
$(x_n, y_n)$
Se construye una sucesión de rectas entre dos puntos continuos. Tomemos por ejemplo los puntos
$(x_1, y_1)$
$(x_2, y_2)$
pendiente $m = \frac{y_2 - y_1}{x_2 - x_1}$, ecuación punto pendiente $y - y_1 = m(x - x_1)$, despejando
$y = m(x - x_1) + y_1$, expandiendo
$y = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) + y_1$
generalizando
$y = \frac {y_{k+1}-y_k}{x_{k+1}-x_k}(x-x_k) + y_k$, esta ecuación nos permite construir una función a trozos para n datos, de n-1 ecuaciones
si se desea consultar el valor de y para algún valor de x en el dominio $[x_0, x_n]$
dado x en $[x_0, x_n]$
k <- 0
mientras ($x_k$ > x) hacer
k <- k + 1
fin
$y = \frac {y_{k-1}-y_{k-2}}{x_{k-1}-x_{k-2}}(x-x_{k-2}) + y_{k-2}$
2.- Lagrange
Orden 1
$f_1(x) = \frac{(x-x_1)}{(x_0-x_1)}y_0 + \frac{(x-x_0)}{(x_1-x_0)}y_1$
Orden 2
$f_1(x) = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0 +$
$f_1(x) = \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}y_1 +$
$f_1(x) = \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}y_2 $
Generalizando -> Orden n
$\sum_{j=0}^{n} {\frac{\prod_{\stackrel {i=0}{i\neq j}}^n {(x-x_i)}}{\prod_{\stackrel{i=0}{i\neq j}}^n {(x_j-x_i)}}} y_j$
3.- Trazadores cuadráticos y cúbicos
Los trazadores cuadráticos y cúbicos se construyen a partir del polinomio de Lagrange de orden 2 y 3 respectivamente. En donde puede darse los casos:
. Si se están construyendo trazadores cúbicos que el último trazador sea cuadrático o lineal
. Si se están construyendo trazadores cuadráticos que el último trazador sea lineal
4.- Mínimos cuadrados
Ilustraremos el método con un ejemplo clásico
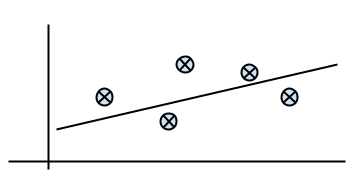
Dado un conjunto de puntos (x, y), se desea hallar la ecuación de la recta con la mejor aproximación, como se muestra en la figura. El modelo que se desea expresar es y = ax+b, en donde a y b son pendiente y corte con el eje vertical respectivamente, pero en definitiva, valores desconocidos.
$$\fbox{$\stackrel{min}{a,b}\sum_{i=0}^{n}{((ax_i+b)-y_i)^2}$}$$
La solución de la ecuación anterior
$\frac{\partial}{\partial a} \sum_{i=0}^{n}{((ax_i+b)-y_i)^2}=-2\sum_{i=0}^{n}{((ax_i+b)-y_i)x_i}$
$\frac{\partial}{\partial b} \sum_{i=0}^{n}{((ax_i+b)-y_i)^2}=2\sum_{i=0}^{n}{((ax_i+b)-y_i)}$
matricialmente podemos escribir el sistema anterior como:
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
El cual se puede resolver por cualquiera de los metodos descritos en la sección de sistemas lineales
Una formula general del error de modelo polinomial de orden igual y superior a 1 se escribe como:
$\sum_{i=0}^{n}{\begin{bmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{bmatrix}}$
observe que para:
con lo cual se genera el modelo polinómico de nuestra preferencia. Las derivadas parciales se obtienen de la siguiente manera
$\frac{\partial}{\partial a_k}\begin{bmatrix}\sum_{i=0}^{n}{\begin{pmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{pmatrix}^2}\end{bmatrix}=\sum_{i=0}^{n}{\begin{pmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{pmatrix}}2{x_i}^{m-k}$
para m = 1
Matricialmente
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
para m = 2
Matricialmente
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} \\ \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i^2 y_i} \\ \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
para m = 3
Matricialmente
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^6} & \sum_{i=0}^{n}{x_i^5} & \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} \\ \sum_{i=0}^{n}{x_i^5} & \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} \\ \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3\end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i^3 y_i} \\ \sum_{i=0}^{n}{x_i^2 y_i} \\ \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
para m = t, k = 0, 1, ..., m. En donde m continua siendo el orden del polinomio interpolante, la matriz de mínimos cuadrados a resolver es: $\begin{bmatrix} \sum_{i=0}^{n}{x_i^{2t}} & \sum_{i=0}^{n}{x_i^{2t-1}} & \cdots & \sum_{i=0}^{n}{x_i^t} \\ \sum_{i=0}^{n}{x_i^{2t-1}} & \sum_{i=0}^{n}{x_i^{2t-2}} & \cdots & \sum_{i=0}^{n}{x_i^{t-1}} \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{i=0}^{n}{x_i^t} & \sum_{i=0}^{n}{x_i^{t-1}} & \cdots & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_t\end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i^t y_i} \\ \sum_{i=0}^{n}{x_i^{t-1} y_i} \\ \vdots \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
Mediante las formulaciones anteriores podemos crear el polinomio de aproximación por mínimos cuadrados del orden deseado. La solución de cualquiera de los sistemas obtenidos podemos obtenerla a través de cualquiera de los métodos expuestos en la sección de sistemas lineales.
5.- Matricial
Debemos tener siempre presente que tenemos un conjunto de puntos y deseamos construir un modelo matemático que se aproxime a este conjunto. Es decir, construir una ecuación que modele la tendencia de dichos puntos. Supongamos que deseamos aproximar el modelo $a_0 log(x^2) + a_1 seno(x) + a_2 \sqrt{x}$
nos basta con construir la matriz
$\begin{bmatrix} log(x_0^2) & seno(x_0) & sqrt{x_0} \\ log(x_1^2) & seno(x_1) & sqrt{x_1} \\ \vdots & \vdots & \vdots\\ log(x_n^2) & seno(x_n) & sqrt{x_n}\end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots\\ y_n \end{bmatrix}$
cuyos coeficientes se calculan resolviendo el sistema lineal con cualquiera de los métodos expuestos en la sección de sistemas lineales.
Esta sección considerará únicamente datos en el plano cartesiano (x,y)
1.- Trazadores lineales
Sea un conjunto de puntos (x,y), esto es
$(x_0, y_0)$
$(x_1, y_1)$
$(x_2, y_2)$
:
:
:
$(x_n, y_n)$
Se construye una sucesión de rectas entre dos puntos continuos. Tomemos por ejemplo los puntos
$(x_1, y_1)$
$(x_2, y_2)$
pendiente $m = \frac{y_2 - y_1}{x_2 - x_1}$, ecuación punto pendiente $y - y_1 = m(x - x_1)$, despejando
$y = m(x - x_1) + y_1$, expandiendo
$y = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) + y_1$
generalizando
$y = \frac {y_{k+1}-y_k}{x_{k+1}-x_k}(x-x_k) + y_k$, esta ecuación nos permite construir una función a trozos para n datos, de n-1 ecuaciones
si se desea consultar el valor de y para algún valor de x en el dominio $[x_0, x_n]$
dado x en $[x_0, x_n]$
k <- 0
mientras ($x_k$ > x) hacer
k <- k + 1
fin
$y = \frac {y_{k-1}-y_{k-2}}{x_{k-1}-x_{k-2}}(x-x_{k-2}) + y_{k-2}$
2.- Lagrange
Orden 1
$f_1(x) = \frac{(x-x_1)}{(x_0-x_1)}y_0 + \frac{(x-x_0)}{(x_1-x_0)}y_1$
Orden 2
$f_1(x) = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0 +$
$f_1(x) = \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}y_1 +$
$f_1(x) = \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}y_2 $
Generalizando -> Orden n
$\sum_{j=0}^{n} {\frac{\prod_{\stackrel {i=0}{i\neq j}}^n {(x-x_i)}}{\prod_{\stackrel{i=0}{i\neq j}}^n {(x_j-x_i)}}} y_j$
3.- Trazadores cuadráticos y cúbicos
Los trazadores cuadráticos y cúbicos se construyen a partir del polinomio de Lagrange de orden 2 y 3 respectivamente. En donde puede darse los casos:
. Si se están construyendo trazadores cúbicos que el último trazador sea cuadrático o lineal
. Si se están construyendo trazadores cuadráticos que el último trazador sea lineal
4.- Mínimos cuadrados
Ilustraremos el método con un ejemplo clásico
Dado un conjunto de puntos (x, y), se desea hallar la ecuación de la recta con la mejor aproximación, como se muestra en la figura. El modelo que se desea expresar es y = ax+b, en donde a y b son pendiente y corte con el eje vertical respectivamente, pero en definitiva, valores desconocidos.
La error cuadrático que existe entre cada punto y la posible recta, paralelo al eje vertical, lo podemos expresar como $e=((ax_i+b)-y_i)^2$, la suma de todos los errores para n puntos la expresamos como, $\sum_{i=0}^{n}{((ax_i+b)-y_i)^2}$, deseamos hallar el valor mínimo de la suma de todos los errores cuadráticos planteados para obtener la mejor aproximación posible, esto es
La solución de la ecuación anterior
$\frac{\partial}{\partial a} \sum_{i=0}^{n}{((ax_i+b)-y_i)^2}=-2\sum_{i=0}^{n}{((ax_i+b)-y_i)x_i}$
$\frac{\partial}{\partial b} \sum_{i=0}^{n}{((ax_i+b)-y_i)^2}=2\sum_{i=0}^{n}{((ax_i+b)-y_i)}$
matricialmente podemos escribir el sistema anterior como:
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
El cual se puede resolver por cualquiera de los metodos descritos en la sección de sistemas lineales
Una formula general del error de modelo polinomial de orden igual y superior a 1 se escribe como:
$\sum_{i=0}^{n}{\begin{bmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{bmatrix}}$
observe que para:
|
|
$\sum_{i=0}^{n}{\begin{bmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{bmatrix}}$ |
|
|
$\sum_{i=0}^{n}{a_0 x_i + a_1}-y_i$ |
|
|
$\sum_{i=0}^{n}{a_0 {x_i}^2 + a_1 x_i + a_2}-y_i$ |
|
|
$\sum_{i=0}^{n}{a_0 {x_i}^3 + a_1 {x_i}^2 + a_2 x_i + a_3}-y_i$ |
con lo cual se genera el modelo polinómico de nuestra preferencia. Las derivadas parciales se obtienen de la siguiente manera
$\frac{\partial}{\partial a_k}\begin{bmatrix}\sum_{i=0}^{n}{\begin{pmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{pmatrix}^2}\end{bmatrix}=\sum_{i=0}^{n}{\begin{pmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{pmatrix}}2{x_i}^{m-k}$
para m = 1
|
|
$\frac{\partial}{\partial a_k}\begin{bmatrix}\sum_{i=0}^{n}{\begin{pmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{pmatrix}^2}\end{bmatrix}$ |
|
|
$\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i + a_1}-y_i\end{pmatrix}2x_i$ |
|
|
$\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i + a_1}-y_i\end{pmatrix}2$ |
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
para m = 2
|
|
$\frac{\partial}{\partial a_k}\begin{bmatrix}\sum_{i=0}^{n}{\begin{pmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{pmatrix}^2}\end{bmatrix}$ |
|
|
$\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i^2 + a_1 x_i + a_2}-y_i\end{pmatrix}2{x_i}^2$ |
|
|
$\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i^2 + a_1 x_i + a_2}-y_i\end{pmatrix}2x_i$ |
|
|
$\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i^2 + a_1 x_i + a_2}-y_i\end{pmatrix}2$ |
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} \\ \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i^2 y_i} \\ \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
para m = 3
|
|
$\frac{\partial}{\partial a_k}\begin{bmatrix}\sum_{i=0}^{n}{\begin{pmatrix}\sum_{j=0}^{m}{a_j {x_i}^{m-j}}-y_i\end{pmatrix}^2}\end{bmatrix}$ |
| $\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i^3 + a_1 x_i^2 + a_2 x_i + a_3}-y_i\end{pmatrix}2{x_i}^3$ | |
| $\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i^3 + a_1 x_i^2 + a_2 x_i + a_3}-y_i\end{pmatrix}2x_i^2$ | |
| $\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i^3 + a_1 x_i^2 + a_2 x_i + a_3}-y_i\end{pmatrix}2x_i$ | |
| $\sum_{i=0}^{n}\begin{pmatrix}{a_0 x_i^3 + a_1 x_i^2 + a_2 x_i + a_3}-y_i\end{pmatrix}2$ |
$\begin{bmatrix} \sum_{i=0}^{n}{x_i^6} & \sum_{i=0}^{n}{x_i^5} & \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} \\ \sum_{i=0}^{n}{x_i^5} & \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} \\ \sum_{i=0}^{n}{x_i^4} & \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} \\ \sum_{i=0}^{n}{x_i^3} & \sum_{i=0}^{n}{x_i^2} & \sum_{i=0}^{n}{x_i} & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3\end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i^3 y_i} \\ \sum_{i=0}^{n}{x_i^2 y_i} \\ \sum_{i=0}^{n}{x_i y_i} \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
para m = t, k = 0, 1, ..., m. En donde m continua siendo el orden del polinomio interpolante, la matriz de mínimos cuadrados a resolver es: $\begin{bmatrix} \sum_{i=0}^{n}{x_i^{2t}} & \sum_{i=0}^{n}{x_i^{2t-1}} & \cdots & \sum_{i=0}^{n}{x_i^t} \\ \sum_{i=0}^{n}{x_i^{2t-1}} & \sum_{i=0}^{n}{x_i^{2t-2}} & \cdots & \sum_{i=0}^{n}{x_i^{t-1}} \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{i=0}^{n}{x_i^t} & \sum_{i=0}^{n}{x_i^{t-1}} & \cdots & {1} \end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_t\end{bmatrix} = \begin{bmatrix} \sum_{i=0}^{n}{x_i^t y_i} \\ \sum_{i=0}^{n}{x_i^{t-1} y_i} \\ \vdots \\ \sum_{i=0}^{n}{y_i} \end{bmatrix}$
Mediante las formulaciones anteriores podemos crear el polinomio de aproximación por mínimos cuadrados del orden deseado. La solución de cualquiera de los sistemas obtenidos podemos obtenerla a través de cualquiera de los métodos expuestos en la sección de sistemas lineales.
5.- Matricial
Debemos tener siempre presente que tenemos un conjunto de puntos y deseamos construir un modelo matemático que se aproxime a este conjunto. Es decir, construir una ecuación que modele la tendencia de dichos puntos. Supongamos que deseamos aproximar el modelo $a_0 log(x^2) + a_1 seno(x) + a_2 \sqrt{x}$
nos basta con construir la matriz
$\begin{bmatrix} log(x_0^2) & seno(x_0) & sqrt{x_0} \\ log(x_1^2) & seno(x_1) & sqrt{x_1} \\ \vdots & \vdots & \vdots\\ log(x_n^2) & seno(x_n) & sqrt{x_n}\end{bmatrix}\begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots\\ y_n \end{bmatrix}$
cuyos coeficientes se calculan resolviendo el sistema lineal con cualquiera de los métodos expuestos en la sección de sistemas lineales.
No hay comentarios:
Publicar un comentario